- 1. Print graphics
- 2. MadLibs
- 3. Calculator
- 4. Applications
- 5. Numbers
- 6. Conjectures
- 7. StudentMIS
- 8. Tickets System
- 9. Sequence List Basic System
- 10. Sequence List Application System
- 11. Link List Basic System
- 12. Link List Application System
- 13. Complexity of Algorithms
- 14. Queue Application System
- 15. Stack Application System
- 16. Sparse Matrix System
- 17. Triangular Matrix System
- 18. Idioms Solitaire(成语接龙)
- 19. Binary Tree System
- 20. Huffman Tree System
- 21. Graph System
- 22. BitOperation
- 23. BigNumber
- More to be coming...

Projects of C++
C++ Programming and Object-Oriented Design
Project 14. Queue Application System
菜单(Press 0 for English Menu)

Menu(按0切换到中文菜单)
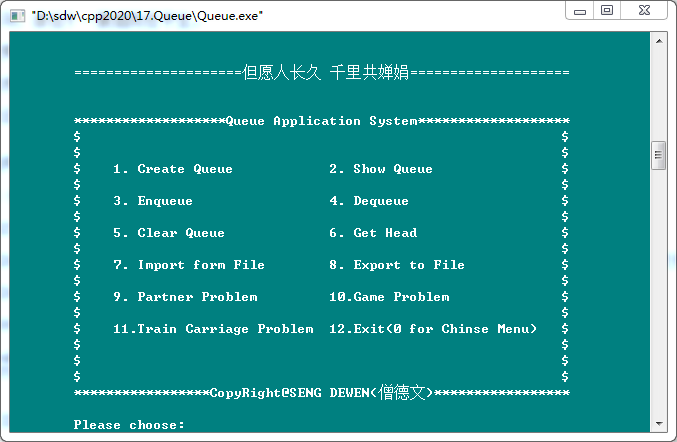
1. Create Queue(创建队列)
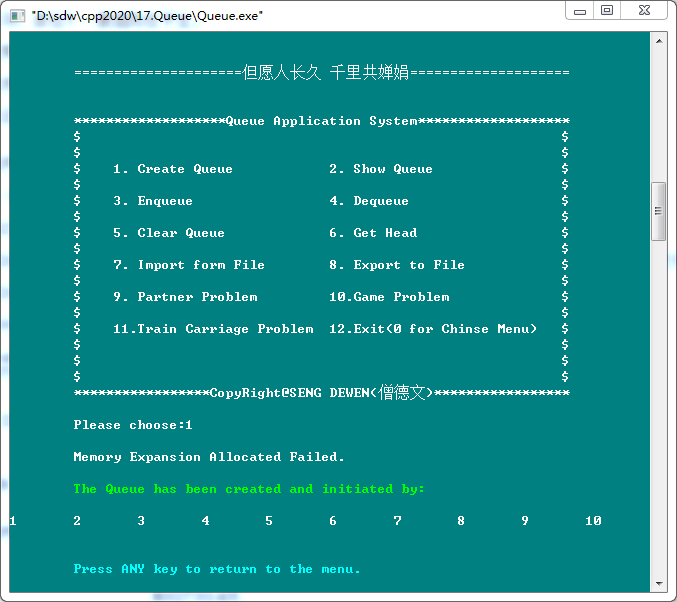
2. Show Queue(显示队列)
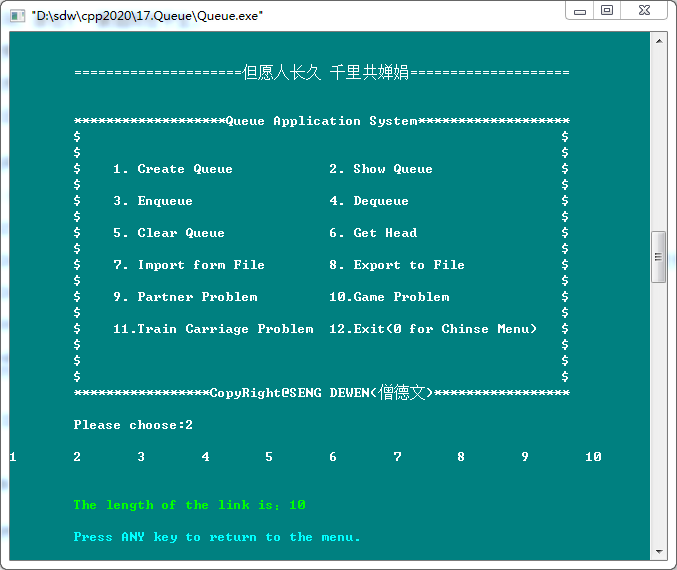
3. Enqueue(入队列)
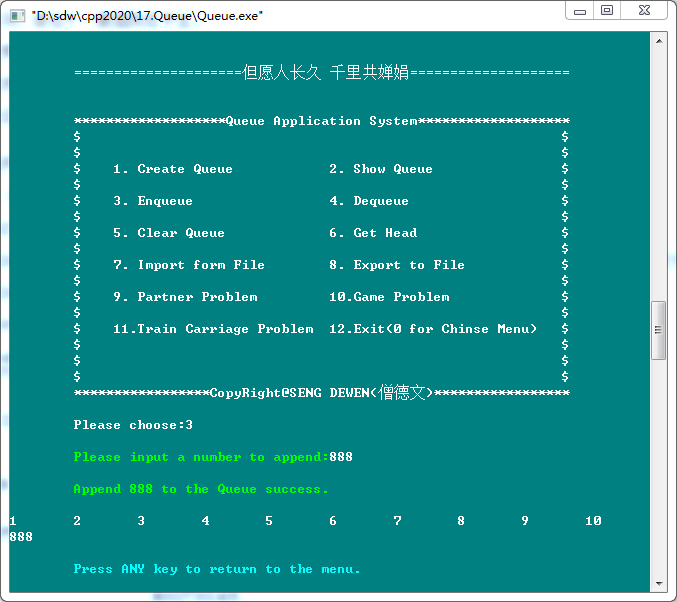
4. Dequeue(出队列)
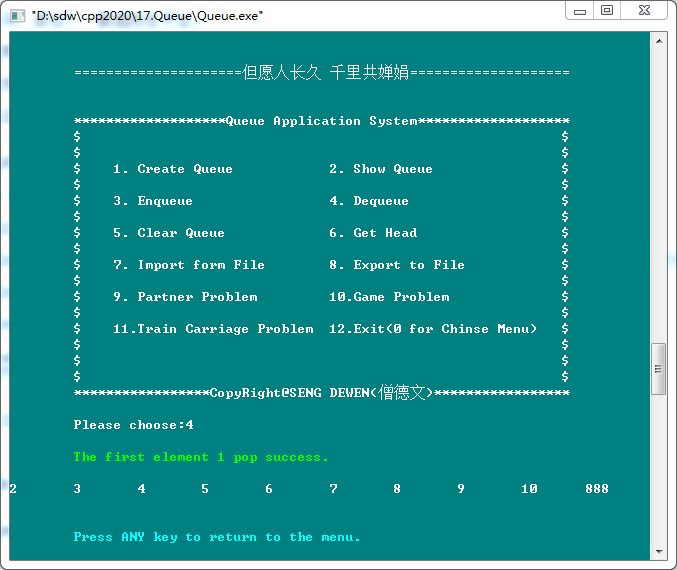
5. Clear Queue(清空队列)
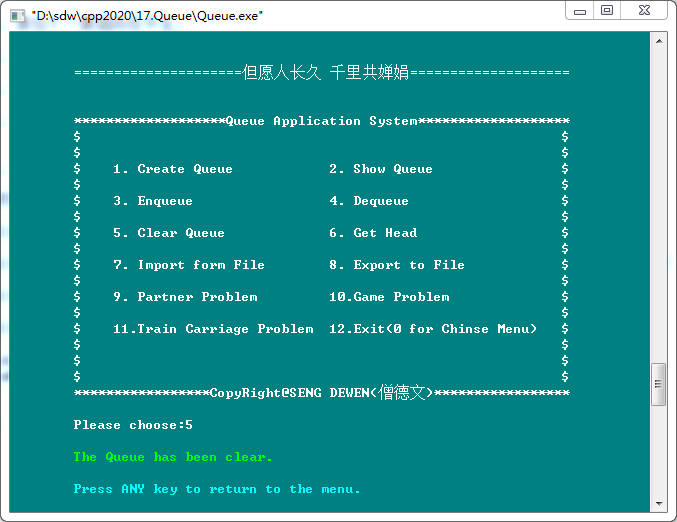
6. Get Head(获取队头元素)
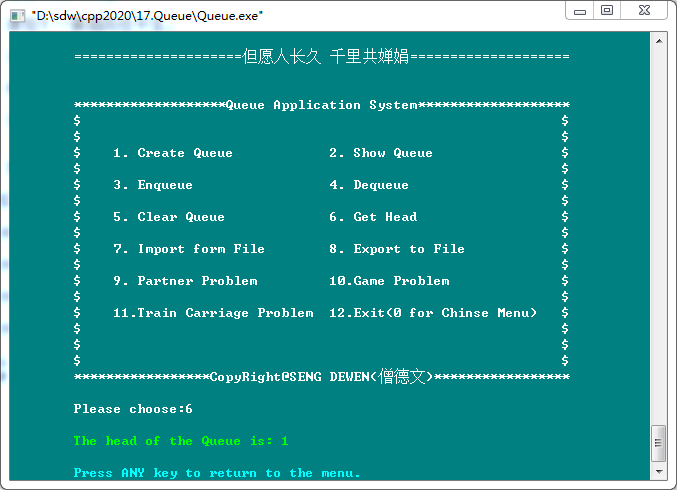
7. Import to File(从文件导入)
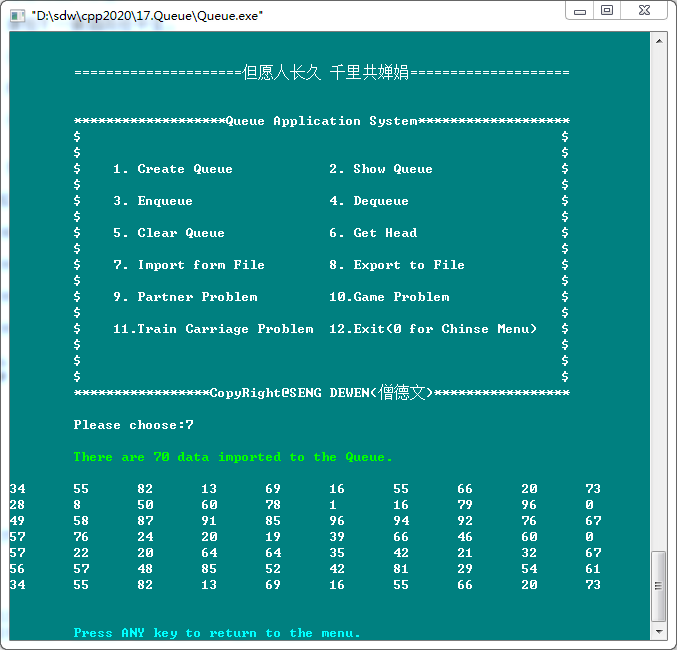
8. Export to File(导出到文件)

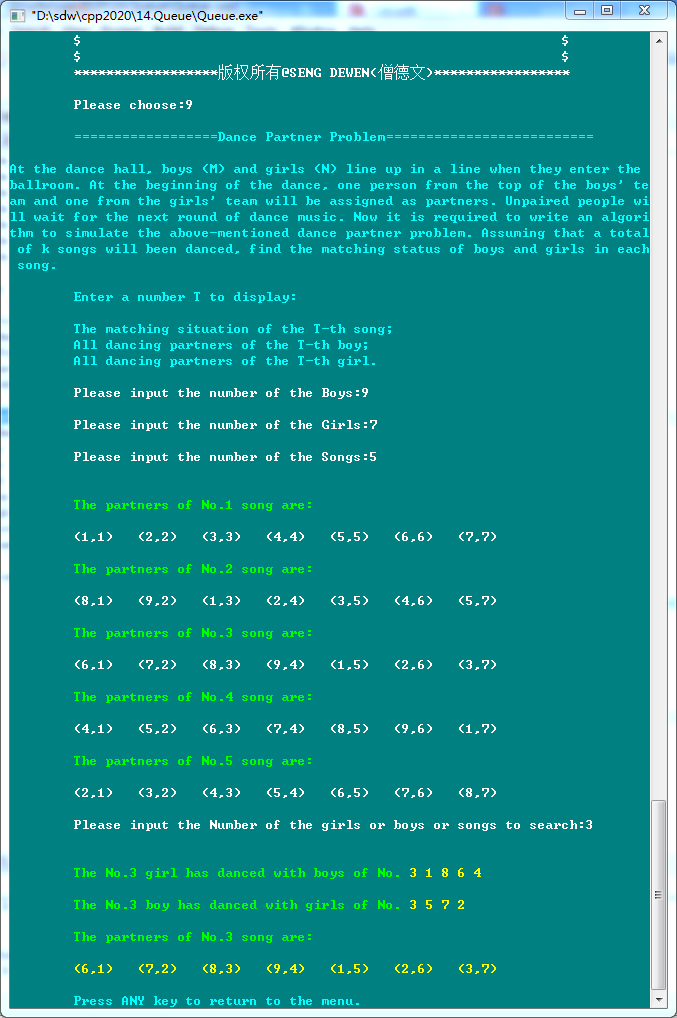
9. Partner Problem(舞伴问题)
At the dance hall, boys (M) and girls (N) line up in a line when they enter the ballroom. At the beginning of the dance, one person from the top of the boys' team and one from the girls' team will be assigned as partners. Unpaired people will wait for the next round of dance music. Now it is required to write an algorithm to simulate the above-mentioned dance partner problem. Assuming that a total of k songs will been danced, find the matching status of boys and girls in each song.
Enter a number t to display:
(1). The matching situation of the t-th song;
(2). All dancing partners of the t-th boy;
(3). All dancing partners of the t-th girl.
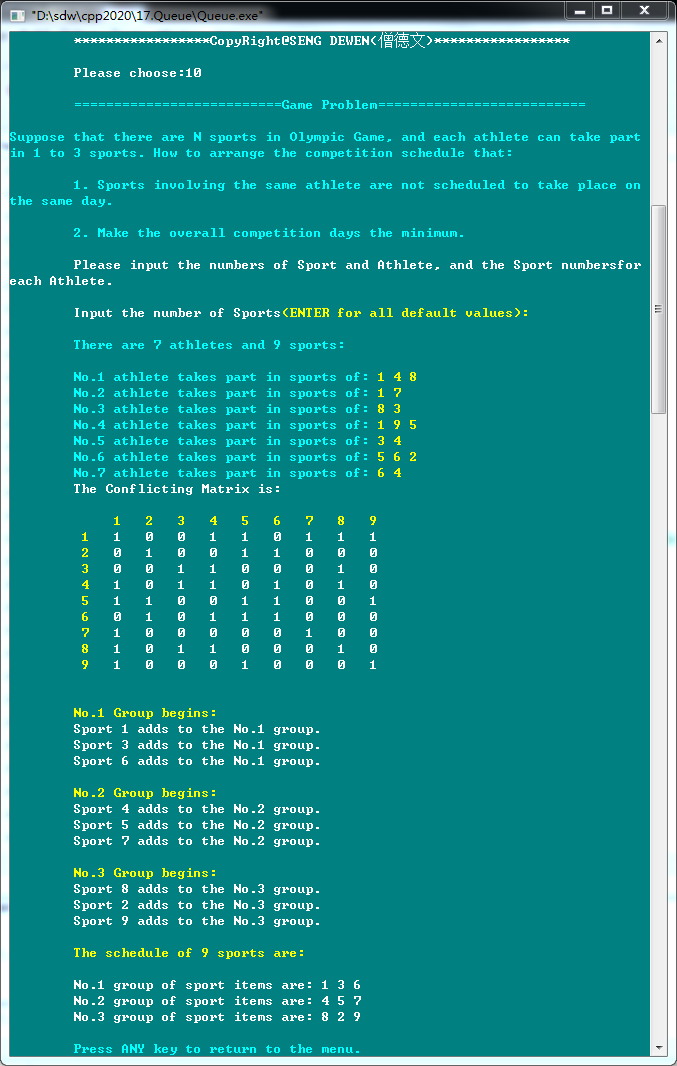
10. Game Problem(运动会问题)
Suppose that there are N sports in Olympic Game, and each athlete can take part in 1 to 3 sports. How to arrange the competition schedule that:
(1). Sports involving the same athlete are not scheduled to take place on the same day.
(2). Make the overall competition days the minimum.
11. Train Carriage Problem(火车车厢问题)
A freight train has N carriages, each of which will be parked at a different station. It is assumed that the serial numbers of N stations (from far to near) are 1-N in order, that is, freight trains pass through these stations in the order from the N-th station to the first station.
In order to facilitate the removal of the respective carriages from the train, the carriages should be arranged the same as those of the stations so that the carriages are in order from front to back, arranged 1 to N, so that only the last carriage is removed at each station.
The Brain Carriages arrive at the station at different times, so they need to be rearranged by using the Buffer Tracks, and then get out in the order of 1-N. Assuming that the amount of Buffer Track is K, it can be judged whether the train carriages arriving at the station can be rearranged successfully or not.
For example:
Suppose there are 3 Buffer Tracks, and the order of arrival of the cars is: 3,6,9,2,4,7,1,8,5, then the order of 1-N rearrangement can be completed.
If the order of arrival of the cars is: 3,6,9,2,4,7,5,8,1, then it is impossible to complete the order of 1-N rearrangement.

12. Exit(退出程序)

|
