Welcome to C++ Program Design!
  For academic exchanges, please add WeChat:  22995321Seng Dewen
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • Hello World!

    Beautiful World, Wonderful Life.

  • Change the World by Program.

  • A language that doesn't affect the way you think about programming, is not worth knowing.

    Alan J. Perlis

  • Mosher's Law of Software Engineering

    Don't worry if it doesn't work right.
    If everything did, you'd be out of a job.

  • Any code of your own that you haven't looked at for six or more months might as well have been written by someone else. (Eagleson's law)
  • Stewart Brand


    Once a new technology starts rolling, if you're
    not part of the steamroller, you're part of the road.

  • Bjarne Stroustrup

    There are only two kinds of programming languages:
    those people always bitch about and those nobody uses.

  • Nine women can't make a baby in one month.

  • Within a computer,
    natural language is unnatural.

  • If you're the smartest person in the room, then

    you're in the wrong room.

  • Without requirements or design,
    programming is the art of adding bugs to an empty text file.

    --Louis Srygley

  • Fools ignore complexity.
    Pragmatists suffer it.
    Some can avoid it.
    Geniuses remove it.

Projects of C++

C++ Programming and Object-Oriented Design

Project 5. Numbers

 

Click to Download the Executable Files.       Click to Download the Sources Files. (Password Needed)

 

Name: Numbers
Copyright: Seng Dewen
Author: Seng Dewen
Date: Sept. 16, 2020
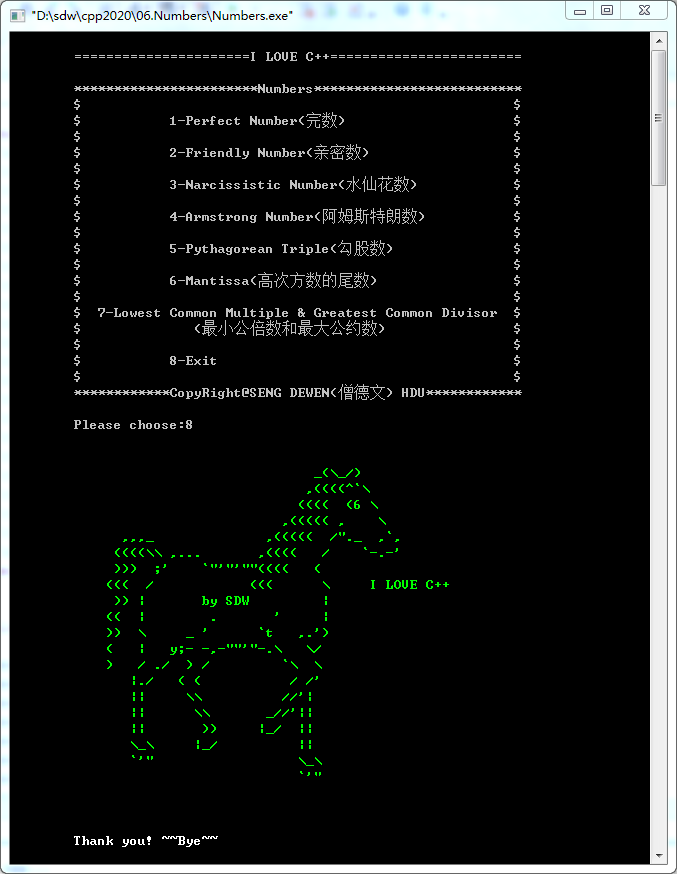
Description: Interesting Numbers.


Menu



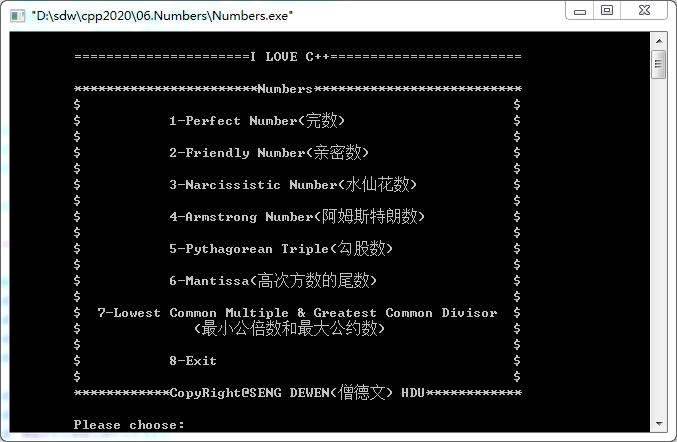
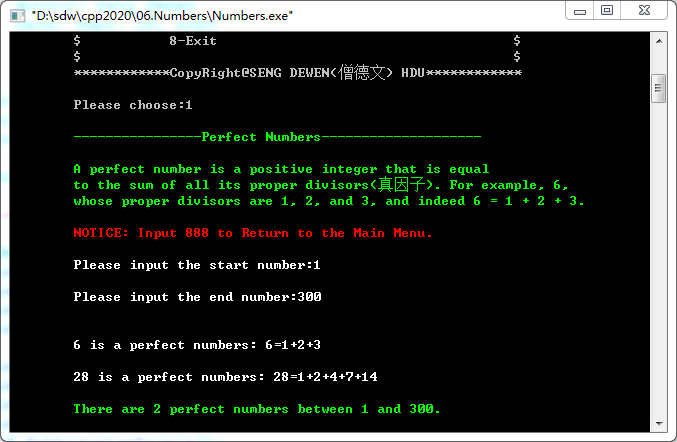
1. Perfect Number(完数)


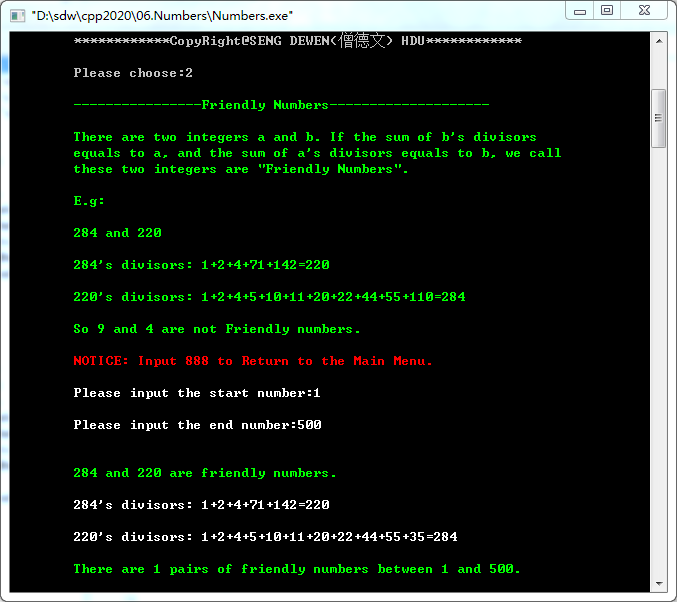
A perfect number is a positive integer that is equal to the sum of all its proper divisors(真因子). For example, 6, whose proper divisors are 1, 2, and 3, and indeed 6 = 1 + 2 + 3.


2. Friendly Number(亲密数)


There are two integers a and b. If the sum of b's divisors equals to a, and the sum of a's divisors equals to b, we call these two integers are "Friendly Numbers".

E.g:

284 and 220

284's divisors: 1+2+4+71+142=220

220's divisors: 1+2+4+5+10+11+20+22+44+55+110=284

So 9 and 4 are not Friendly numbers.



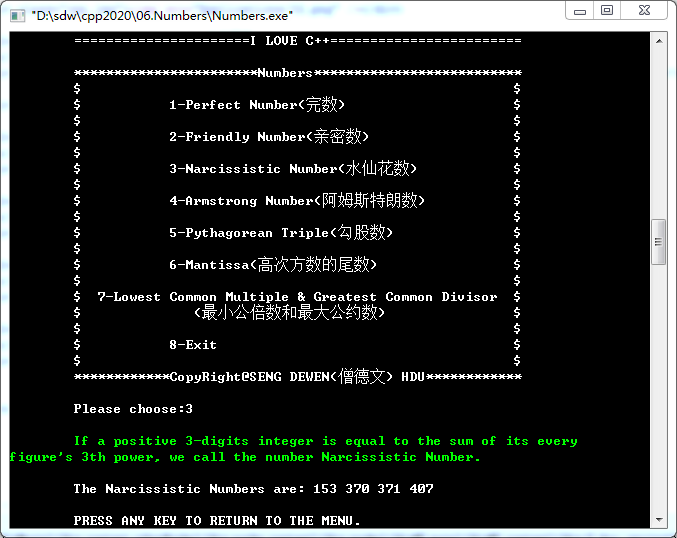
3. Narcissistic Number(水仙花数)


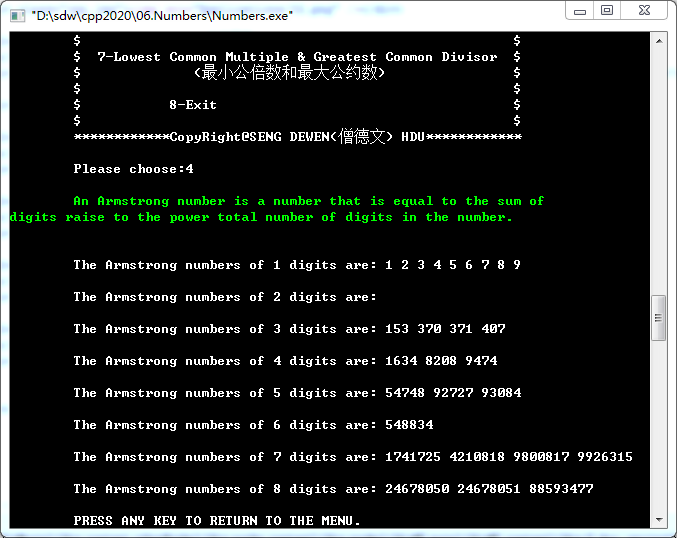
If a positive 3-digits integer is equal to the sum of its every figure's 3th power, we call the number Narcissistic Number. The Narcissistic Numbers are: 153 370 371 407


4. Armstrong Number(阿姆斯特朗数)


An Armstrong number is a number that is equal to the sum of digits raise to the power total number of digits in the number.

--The Armstrong numbers of 1 digits are: 1 2 3 4 5 6 7 8 9

--The Armstrong numbers of 2 digits are:

--The Armstrong numbers of 3 digits are: 153 370 371 407

--The Armstrong numbers of 4 digits are: 1634 8208 9474

--The Armstrong numbers of 5 digits are: 54748 92727 93084

--The Armstrong numbers of 6 digits are: 548834

--The Armstrong numbers of 7 digits are: 1741725 4210818 9800817 9926315

--The Armstrong numbers of 8 digits are: 24678050 24678051 88593477


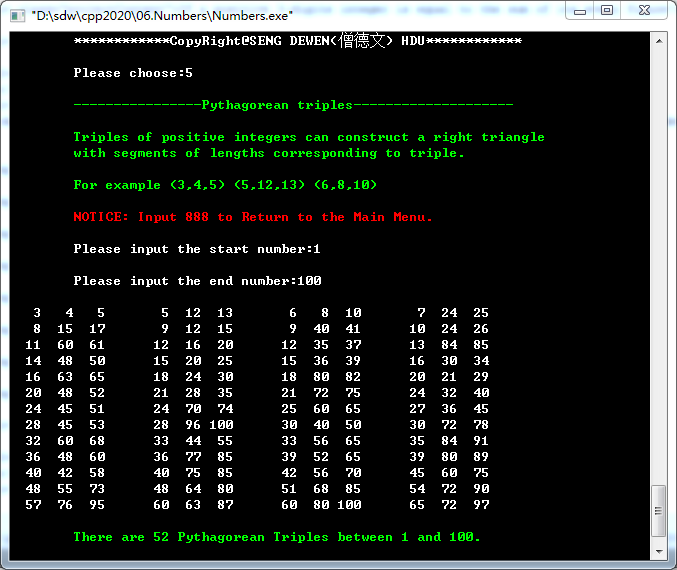
5. Pythagorean Triple(勾股数)


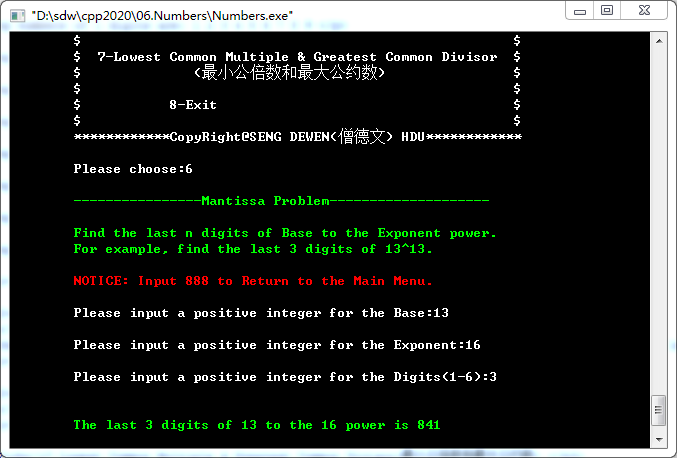
Pythagorean triples: Triples of positive integers can construct a right triangle with segments of lengths corresponding to triple. For example (3,4,5) (5,12,13) (6,8,10)


6. Mantissa(高次方数的尾数)


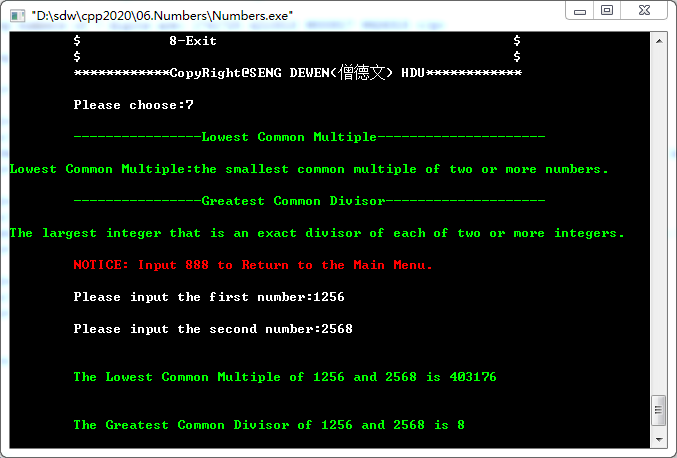
Mantissa Problem: Find the last n digits of Base to the Exponent power. For example, find the last 3 digits of 13^13.


7.Lowest Common Multiple & Greatest Common Divisor(最小公倍数和最大公约数)


Lowest Common Multiple: Lowest Common Multiple:the smallest common multiple of two or more numbers.

Greatest Common Divisor: The largest integer that is an exact divisor of each of two or more integers.


8.Exit


 

 

 

Back to Top

 

桃李无言，下自成蹊 @僧德文 Copyright © 2010-2022 All Rights Reserved. Seng Dewen For academic exchanges, please add WeChat: 22995321